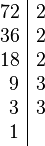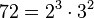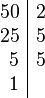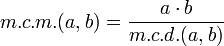Mínimo común múltiplo

De Wikipedia, la enciclopedia libre

El mínimo común múltiplo (m.c.m.) de dos o más números naturales es el menor número natural que es múltiplo de todos ellos. Sólo se aplica con números naturales, es decir, no se usan decimales ni números negativos.

Cálculo del m.c.m

Partiendo de dos o más números y por descomposición en factores primos, expresados como producto de factores primos, su mínimo común múltiplo será el resultado de multiplicar los factores comunes y no comunes elevados a la mayor potencia, por ejemplo el mcm de 72 y 50 será:

$\begin{array}{r|l} 72 & 2 \\ 36 & 2 \\ 18 & 2 \\ 9 & 3 \\ 3 & 3 \\ 1 & \end{array}$

$72 = 2^3 \cdot 3^2 \,$

$\begin{array}{r|l} 50 & 2 \\ 25 & 5 \\ 5 & 5 \\ 1 & \end{array}$

$50 = 2 \cdot 5^2 \,$

Tomando los factores comunes y no comunes con su mayor exponente, tenemos que:

$mcm (72, 50) = 2^3 \cdot 3^2 \cdot 5^2 = 1800$

Conociendo el máximo común divisor de dos números, se puede calcular el mínimo común múltiplo de ellos, que será el producto de ambos dividido entre su máximo común divisor.

$m.c.m.(a, b) = \frac {a \cdot b}{m.c.d.(a, b)}$

Además podemos utilizar otro método en caso que hubiéramos calculado el máximo común divisor, en el cual se toman los factores comunes y no comunes con el mayor exponente y se multiplican: 2x2 x3 x5 = 60. El m.c.m. de 4, 5 y 6 es 60.

Matematica escolar

miércoles, 20 de octubre de 2010

(M.C.M)

Mínimo común múltiplo

Cálculo del m.c.m

Tabla de numeros primos hasta el 200